My research in tensors is closely related to the phenomena that a given tensor can fail to have a best low rank approximation. At its core, this phenomena is caused by the geometry of the set of rank 1 tensors. Here we use a toy example to illustrate how the geometry of the set of rank 1 tensors causes this behavior.
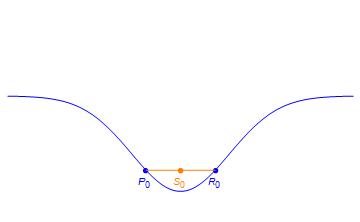
Suppose the ambient space of tensors we are interested in is the 2d plane and the set of rank 1 tensors is the blue curve below.

The rank of a tensor T is the minimal number of rank one tensors which recover T through linear combinations. So in this toy example, the set of rank 2 tensors is the set of tensors which are on a line which passes through two points on the blue curve. For example, the point S0 has rank 2 since it is on the line between P0 and R0.
Not every tensor in this space has rank 2 or less. For example, the point T below does not lie on a line which passes through two points on the blue curve.
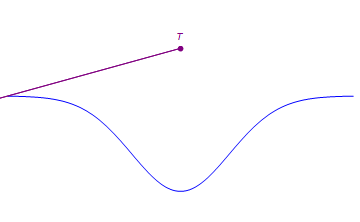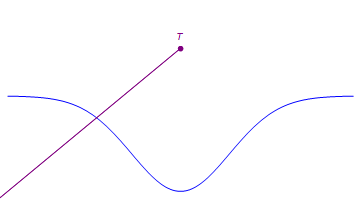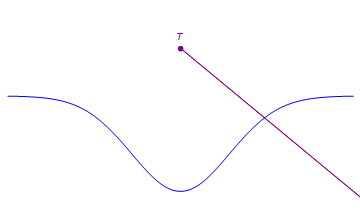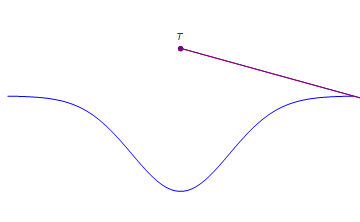
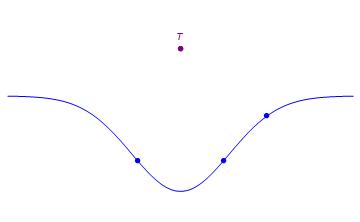
In this example, T has rank 3. In fact, every tensor in this space has rank 3 or less since any three noncolinear points span the 2d plan through linear combinations. E.g., T can be expressed as a linear combination of the points below.
A particularly interesting behavior occurs on the boundary between the sets of rank 2 and rank 3 tensors. As it turns out, there are limits rank of 2 tensors which have rank strictly greater than 2. Consider the point X below.
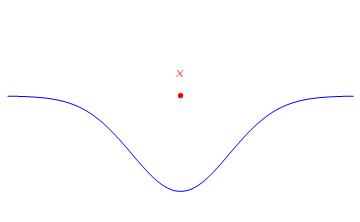
X can be expressed as a limit of rank 2 tensors in the following way.
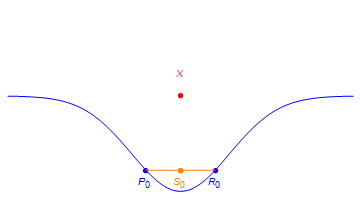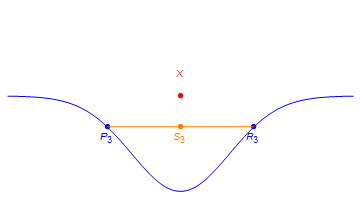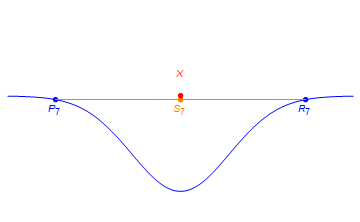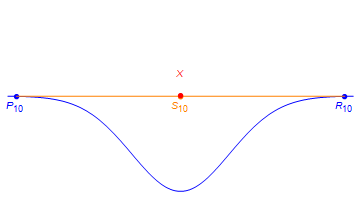
In particular, if one defines sequences Pn and Rn as in the figure and sets Sn = (Pn+Rn)/2, then X is the limit of the Sn as n approaches infinity. However, X does itself does not have rank 2.
Very commonly in applications, one encounters a data set which can be modeled as a noisy measurement of a low rank tensor. By decomposing the underlying signal tensor as a sum of rank one terms, one can extract interpretable component information from the data set. However, the issues discussed above can pose big challenges for this approach.
Suppose one wishes to extract rank 2 component information given the measured tensor X. Based on the above discussion, one can almost exactly approximate X by the rank 2 tensor Sn when n is taken sufficiently large. However, for very large n, the underlying rank 1 components Pn and Rn communicate very little information. In particular, as n grows large, the magnitudes of Pn and Rn both approach infinity. Furthermore, for very large n, Pn is approximately equal to -Rn. This behavior is called diverging components, and it necessarily occurs if a given tensor does not have a best low rank approximation.
One major goal in my tensors based research is the development of perturbation theoretic bounds which guarantee the existence of best low rank approximations. These bounds in turn guarantee that undesirable effects such as diverging components do not occur.